andycrellin posted an inquiry on the board of the Flowing Data, regarding software for drawing so-called source-destintation split diagrams. Nathany answered pointing to the Sankey software list on this blog. Thanks!
This is andy’s colorful sample. Quite nice. I especially like the color gradients along the bands, a feature which – to my knowledge – none of the software tools currently supports.
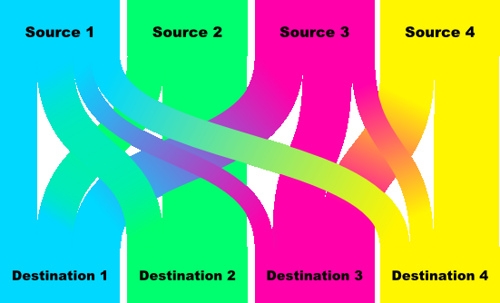
1 Comment
Sankey Editor does the Color Gradient!
K
Comments are closed.