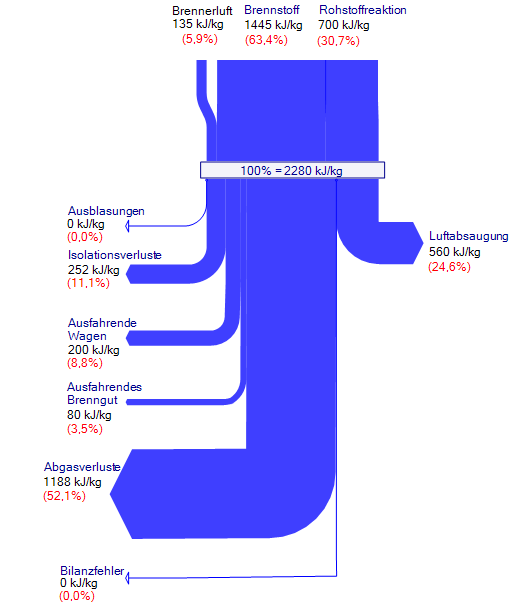
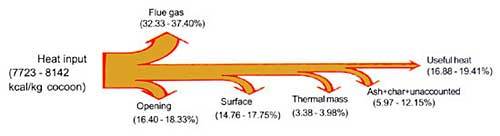
Here are two Sankey diagrams that show the energy losses in an industrial ceramic furnace. The diagrams are oriented top-down. The labels are in German.
The Sankey diagram in blue shows the energy use in an industrial ceramic furnace. The flows are shown in absolute values and in percentage values.
The second diagram in red is similar to the blue one, but it only show the relative flows in percentiles. Additionally the flows entering the diagram at the top have been separated to show their shares. Other flows (‘Rest’) have been grouped together and the individual contributions are shown on the label.